목차
0. Overview
이 글에서는 고차원 자료를 위한 이상치 탐지 기법의 주된 동기가 되는 현상인 집중효과 (Concentration Effect)를 소개하고 이러한 집중효과를 방지하기 위해 어떠한 접근법이 고려될 수 있는지 설명하고자 합니다. 이 글을 읽음으로써 다음 질문들에 대한 답을 얻어가실 수 있습니다.
- 집중효과 (Concentration Effect)란 무엇인가?
- 집중효과가 이상치 탐지에 미치는 영향은 무엇인가?
- 집중효과를 방지할 수 있는 (일반화된) 접근법은 무엇인가?
1. Introduction
무엇이든 결론부터 이야기하는게 좋지 않습니까? 위의 질문에 대한 답을 먼저하고 자세한 설명은 본문에서 다루도록 하겠습니다.
- 집중효과 (Concentration Effect)란 무엇인가?
- 집중효과는 변수가 추가됨에 따라 관측치들간의 (변수공간상) 거리가 모두 비슷해지는 현상이다.
- 이러한 현상이 나타나는 이유는 변수가 추가될수록 관측치들간의 거리가 멀어져 거리의 대비 (contrast)가 줄어들기 때문이다.
- 이러한 집중효과는 자료가 특정 조건을 만족할 때 발생한다. 하지만 그 조건이 매우 광범위하기 때문에 오히려 집중효과가 발생하지 않는 경우가 특수한 상황이라고 할 수 있다.
- 변수의 개수가 많은 고차원 자료는 집중효과를 유발하기 쉽다.
- 집중효과가 이상치 탐지에 미치는 영향은 무엇인가?
- 전통적인 (비지도) 이상치 탐지 기법은 관측치들간의 떨어진 거리에 기반해 이상정도 (degree of outlierness)를 정의한다.
- 계산된 이상정도를 기반으로 다른 관측치들과 비교해 높은 값을 가지는 소수의 관측치를 이상치로 판단한다.
- 그런데, 고차원 자료의 경우 집중효과로 인해 관측치들간의 거리가 모두 비슷해져 이상치와 다른 관측치들간의 거리의 대비가 줄어들기 때문에 이상치를 명확하게 탐지하지 못하는 문제가 발생한다.
- 집중효과를 방지할 수 있는 (일반화된) 접근법은 무엇인가?
- 집중효과가 발생하지 않는 경우를 일반화해서 나타내면 다음과 같다.
- 자료가 분리 가능한 클러스터(separable cluster) 구조를 가지는 경우
- 변수간의 상관관계가 강한 경우
- 집중효과가 발생하지 않는 경우를 일반화해서 나타내면 다음과 같다.
고차원 자료에서의 이상치 탐지는 위와 같은 이유로 인해 집중효과를 극복할 수 있는 접근을 필요로 합니다. 부분공간 이상치 탐지(Subspace Outlier Detection)는 위와 같은 동기에 기반해 제안된 대표적인 기법입니다. 이 방법은 자료의 전체 변수 중 특정 기준을 만족하는 변수들을 선별하여 형성한 부분공간(subspace)에서 관측치의 이상정도를 측정함으로써 고차원 자료에서의 집중효과를 극복합니다. (부분공간 이상치 탐지에 대한 내용은 다음 글에서 자세히 작성하도록 하겠습니다.)
2. Concentration Effect(집중효과)
이 장에서는 집중효과를 소개하고 이 현상이 의미하는 바와 이에 대한 핵심 질문을 제시합니다.
Notation
집중효과를 설명하는데 사용하는 표기법(notation)을 다음과 같이 정의합니다.

Theorem1. Concentration Effect
위의 정의에 기반해 집중효과를 다음과 같이 나타낼 수 있습니다.

이 때, $E[\cdot]$와 $Var[\cdot]$은 각각 확률변수의 이론적 기대값과 분산을 의미합니다. 그리고 $\rm{E}[d_{m,p}(\boldsymbol{X}^{(m)},\boldsymbol{Q}^{(m)})]$와 $\rm{Var}(d_{m,p}(\boldsymbol{X}^{(m)},\boldsymbol{Q}^{(m)}))$는 유한한 값을 가지며 $\rm{E}[d_{m,p}(\boldsymbol{X}^{(m)},\boldsymbol{Q}^{(m)})]\ne 0$ 임을 가정합니다.
Theorem 1을 통해 특정한 조건이 만족하면, 관측치간의 거리의 최소값 $DMIN^{(m)}$과 최대값 $DMAX^{(m)}$의 비율이 차원 (m)이 커짐에 따라 1로 확률수렴함을 알 수 있습니다. 즉, 변수 (차원)의 개수가 무한대로 커질 때 모든 관측치들의 거리가 같아지는 것이죠. (Theorem 1에 대한 증명은 이 글의 주제를 벗어납니다. 이에 대한 증명은 후에 따로 작성하도록 하겠습니다.)
Theorem 1의 조건이 의미하는 바를 살펴보죠. Theorem 1의 조건 즉,

는 무엇을 의미할까요?
차원 m이 무한대로 커질 때, 분모에 위치한 "거리의 기댓값의 제곱"이 커지는 속도가 분자에 위치한 "거리의 분산"이 커지는 속도보다 더 빠름을 나타냅니다. 거리 함수를 떠올려보죠. 우리는 $d_{m,p}$를 $L_{p}$ 거리로 정의했습니다. 따라서 $d_{m,p}(\boldsymbol{X},\boldsymbol{Q})$ = $\sum_{j=1}^{m}|X_{j} - Q_{j}|^{p}$ 로 나타낼 수 있습니다. 차원이 커짐에 따라 거리를 더해나가기 때문에 $d_{\ell, p}(\boldsymbol{X},\boldsymbol{Q}) \geq d_{t, p}(\boldsymbol{X},\boldsymbol{Q}), \; \text{for } \ell > t$가 항상 성립함을 알 수 있습니다. 그러니까 차원이 추가될수록 관측치들간의 떨어진 거리는 점점 더 증가하는 것이죠. 이 때, 만약 거리의 기댓값의 제곱이 거리의 분산보다 증가하는 속도가 빠르면 Theorem1의 조건이 만족하여 집중효과가 발생한다는 것을 알 수 있습니다.
Immediate Questions
Theorem 1을 보고 떠오르는 즉각적인 의문 혹은 질문은 다음과 같습니다.
- Theorem 1의 조건은 "언제 성립"하나?
- 답변) 다음 섹션에서 조건을 만족하는 경우와 그렇지 않은 경우를 소개하고 이에대한 증명과 실험결과를 제시합니다.
- 조건이 만족한다면, 차원이 추가됨에 따라 "어느정도 속도"로 모든 관측치들의 거리가 비슷해지나?
- 답변) 이 문제는 이론적으로 접근하기 어렵습니다. 따라서 역시 각 상황에 대한 실험결과를 통해 확인합니다.
3. Applicability of Concentration Effect
이 섹션에선 집중효과의 조건이 만족하는 경우와 그렇지 않은 경우를 case by case로 소개하고 이에 대한 증명 및 실험 결과를 제시합니다.
Case 1) IID Dimensions with Query and Data Independence
모든 변수가 IID (identical and independently distributed)인 경우.
(예, $X_{1}, X_{2}, \cdots, X_{m} \sim N(0,1)$)

위 증명을 통해 모든 변수가 IID인 경우 분포에 관계없이 집중효과의 조건이 만족함을 확인할 수 있습니다.
Case 2) Marginal Data and Query Distributions Change with Dimensionality
각 변수가 같은 분포를 따르지 않는 경우
(예, $X_{1} \sim N(0,1), X_{2} \sim Unif(0,1), \cdots, X_{m} \sim Exp(1)$

각 변수가 같은 분포를 따르지 않는 경우에도 집중효과의 조건이 만족합니다.
이에 대한 증명은 이 글에서 다루지 않고 실험을 통해 보입니다.
Case 3) Identical Dimensions with no Independence
모든 변수가 동일한 분포를 따르지만 완전히 의존적인 (completely dependent)한 경우 (즉, 모든 변수간의 상관계수가 1인경우)
(예, $X_{1} = X_{2} = \cdots = X_{m}$)

위 증명을 통해 모든 변수가 완전히 의존적인(completely dependent) 경우 집중효과의 조건이 "만족하지 않음"을 확인할 수 있습니다.
Experimental Results
앞에서 제시한 상황에 대응하는 자료를 생성하여 측정한 $log(DMAX/DMIN)$의 결과를 나타내면 다음과 같습니다.
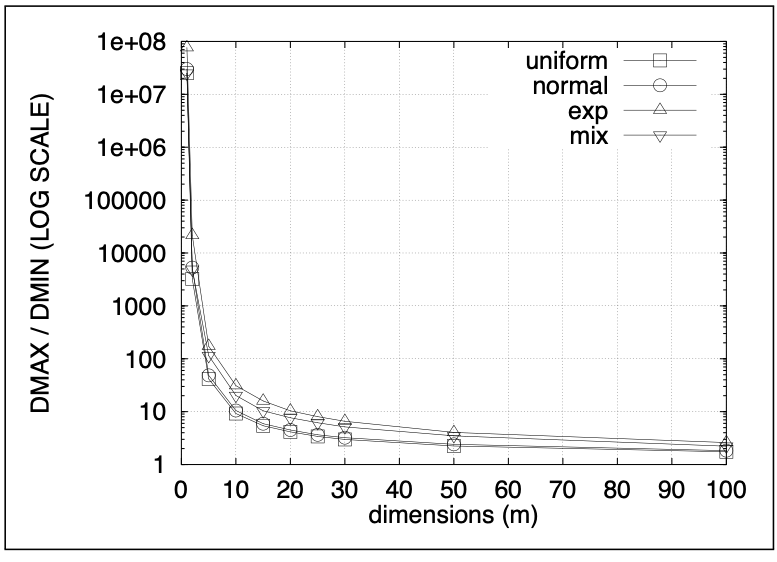

그림1의 좌측 그림에서 'uniform', 'normal', 'exp'는 모두 Case 1의 IID 조건이 만족하는 경우를 의미합니다. 즉, normal의 경우 $X_{1}, X_{2}, \cdots, X_{3} \sim N(0,1)$을 나타냅니다. 한편, mix는 Case 2의 각 변수가 각기 다른 분포를 따르는 경우를 나타냅니다. 이 때, 각 변수는 uniform, normal, exponential 분포 중 하나를 임의로(randomly) 선정하였습니다. 그림을 통해 uniform, normal, exp, mix 모든 상황에서 log(DMAX/DMIN)의 값이 차원이 커짐에 따라 작아지는 것을 확인할 수 있습니다. 또한 차원 크기가 15에서 20정도만 되더라도 거리의 대비가 매우 작아짐으로 집중효과의 수렴속도가 빠름을 알 수 있습니다.
그림1의 우측 그림에서 'two degree of freedom'은 Case 3의 모든 변수가 완전히 의존적인 경우를 나타냅니다. 이 경우 차원이 커짐에도 불구하고 log(DMAX/DMIN)의 값이 줄어들지 않는 것을 확인함으로써 집중효과가 발생하지 않는 것을 관측할 수 있습니다.
P.S. 이상치(outlier)가 존재하는 경우의 집중효과
우리는 본문에서 이상치의 여부를 고려하지 않았습니다. 만약 자료에 이상치가 존재하는 경우엔 어떤 양상을 보일까요? 이를 보이기 위해 간단한 실험 결과를 제시합니다. 실험 세팅은 아래와 같습니다.
- $X_{1}, X_{2}, \cdots, X_{m} \sim N(0,1)$을 따르는 서로 독립인 $m$개의 확률변수에 대하여 $n = 1000$개의 임의 표본을 생성하여 자료를 구성한다. 자료에서 $x_{11}=10$로 두어 첫번째 관측치 $x_{1}$이 첫번째 변수로 인하여 이상치가 되는 경우를 상정한다
- 위의 자료에 대표적인 비지도 이상치 탐지 기법인 LOF를 적용하여 각 관측치 $x_{i}, \; i \leq n$의 이상정도를 측정한다.

그림4를 통해 $m$의 크기가 작을 때는 $x_{1}$의 이상정도가 다른 관측치의 이상정도보다 매우 크지만 $m$의 크기가 커지면 $x_{1}$과 다른 관측치의 이상정도의 대비가 매우 줄어드는 것을 확인할 수 있습니다.
4. Generalized Cases that Prevent Concentration Effect
앞에서 세가지 상황에 대한 증명과 실험을 통해 집중효과의 조건이 만족하는 경우와 그 양상을 살펴봤습니다. 이를 통해, 다양한 (IID 가정보다 넓은) 상황에서 집중효과가 발생함을 확인하였고 변수간의 완전한 의존성이 있는 경우 집중효과가 나타나지 않음을 관측했습니다. 이 장에선, 집중효과의 조건이 만족하지 않는 경우를 일반화해서 제시합니다.
Separable Cluster Structure
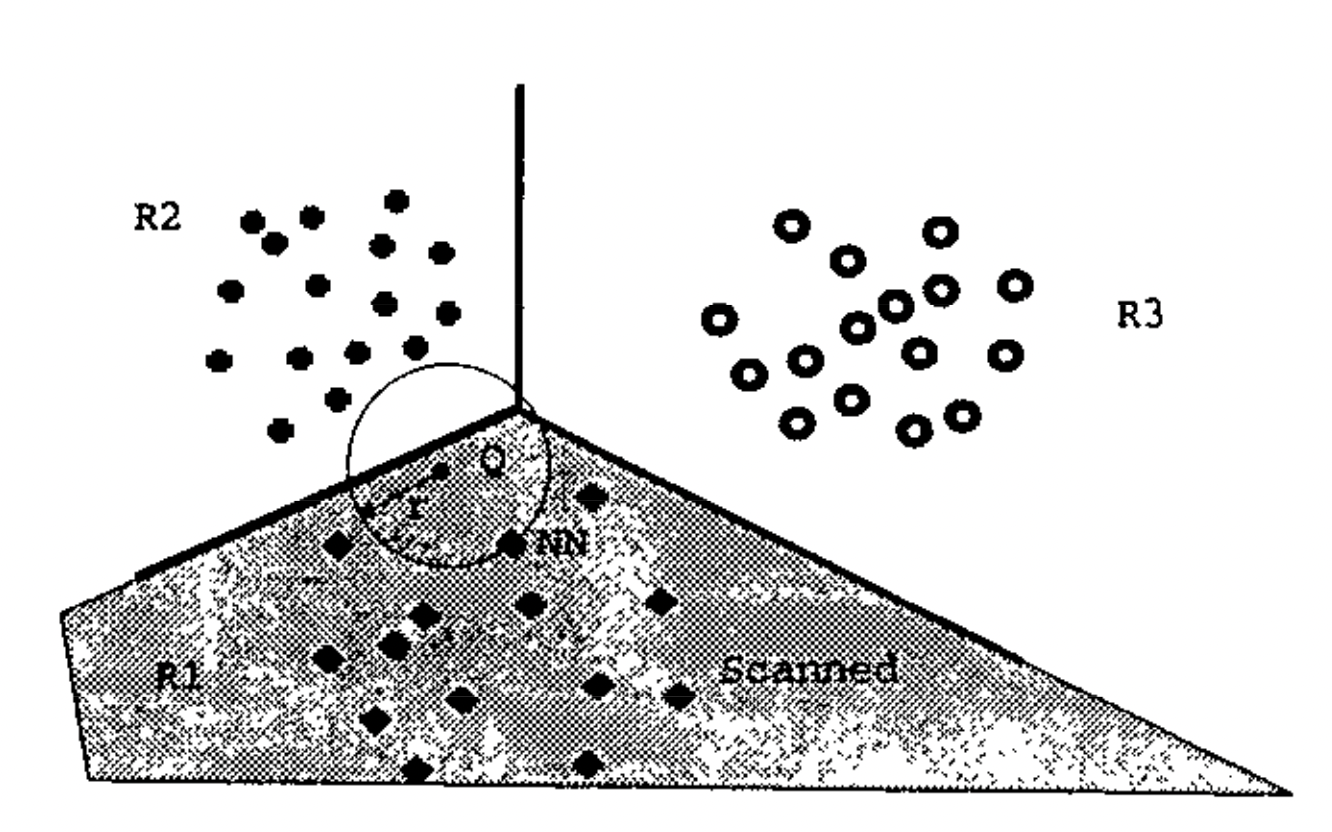
Bennett et. al. [1999]는 분리 가능한 클러스터 구조(separable cluster structure)가 존재하는 경우 각기 다른 클러스터에 속한 점들간의 거리인 "between cluster distance"가 동일한 클러스터에 속한 점들간의 거리인 "within cluster distance"보다 항상 큼을 보임으로써 집중효과가 나타나지 않음을 증명합니다.
(분리 가능한 클러스터에 대한 정의는 Bennett et. al. [1999]를 참고하여 주시기 바랍니다. 참고를 위해 아래 그림2를 첨부합니다.)
Low Intrinsic Structure
Durrant와 Kaban [2009]는 잠재변수 모형(latent variable model)을 이용해서 변수간의 강한 상관관계가 존재할 때 집중효과의 조건이 만족하지 않음을 보입니다. 이는 앞에서 살펴본 Case 3를 일반화한 것이라고 생각할 수 있습니다.
또한 Durrant와 Kaban은 잠재변수 모형의 관점에서 다른 변수와 강한 상관관계를 가지는 변수를 "적합한 차원 (relevant dimension)"로 정의합니다. 아래 그림3은 전체 차원 중 적합한 차원의 비중에 따라 집중효과의 정도가 달라짐을 나타냅니다.

이를 통해 자료에 적합한 차원이 아닌 변수 (부적합한 차원)가 많이 포함될수록 집중효과가 뚜렷하게 나타남을 알 수 있습니다.
5. Conclusion
우리는 본문에서 집중효과가 무엇인지 알아보고 어떤 상황에서 어떤 양상으로 나타나는지 증명과 실험을 통해 살펴봤습니다. 또한 집중효과가 발생하지 않는 일반화된 경우를 알아봤습니다. 이를 통해 우리는 앞서 제기한 질문에 대한 답을 할 수 있게 되었습니다.
- 집중효과 (Concentration Effect)란 무엇인가?
- 집중효과가 이상치 탐지에 미치는 영향은 무엇인가?
- 집중효과를 방지할 수 있는 (일반화된) 접근법은 무엇인가?
References
[1] Beyer, K., Goldstein, J., Ramakrishnan, R., & Shaft, U. (1999, January). When is “nearest neighbor” meaningful?. In International conference on database theory (pp. 217-235). Springer, Berlin, Heidelberg.
[2] Bennett, K. P., Fayyad, U., & Geiger, D. (1999, August). Density-based indexing for approximate nearest-neighbor queries. In Proceedings of the fifth ACM SIGKDD international conference on Knowledge discovery and data mining (pp. 233-243).
[3] Durrant, R. J., & Kabán, A. (2009). When is ‘nearest neighbour’meaningful: A converse theorem and implications. Journal of Complexity, 25(4), 385-397.



