Extended Isolation Forest 논문 리뷰
2018년에 발표된 Extended Isolation Forest 논문을 바탕으로 정리한 글입니다.
본문의 표현은 원문의 내용을 참고하여 작성하였습니다.
(Hariri, Sahand, Matias Carrasco Kind, and Robert J. Brunner. ”Extended isolation forest.” arXiv preprint arXiv:1811.02141 (2018).)
Contents
-
Motivation
-
What Makes This Problem?
-
Solution
-
Notation
-
Methodology
-
Empirical Results
-
Summary
Introduction
Extended Isolation Forest 는 Isolation Forest(2008, Liu) 에서 생기는 문제점을 보완한 anomaly detection 테크닉 입니다. (Isolatoin Forest 에서 사용된 방법을 바탕으로 설명하기 때문에 개념이 생소하신 분은 이전 글 Isolation Forest을 먼저 읽으시길 권합니다.)
기존 Isolation Forest
Isolation Forest는 feature space를 recursive하게 random partition 하는 iTree를 여러개의 subsample들에 대하여 건설한 다음, 만들어진 iTree를 전부 사용해 iForest를 도출하여 각 observation마다의 anomaly score를 계산하는 방법론 이었습니다. Isolation Forest는 computational cost가 효율적이고 anomaly detecting 성능이 좋다는 장점이 있었습니다.
Extended Isolation Forest
Extended Isolation Forest는 기존 Isolation Forest 구조를 바꾸지 않고 그대로 사용합니다. 다만, 차이점은 iTree 건설에 사용되는 random split의 형태를 약간 변형했다는 것입니다. 기존의 random split은 모든 변수 중에서 특정 변수 하나를 random하게 선택하고 그 때의 변수가 가지는 값의 범위 중 특정 값 하나를 random하게 채택하여 split rule을 세워서 이를 만족하는 observation들은 노드의 왼쪽으로 보내고 그렇지 않은 샘플들은 오른쪽으로 보내는 방식으로 작동했습니다. 그렇기 때문에 이 때의 split은 항상 특정 축에 평행한 "axis-parallel split" 이었습니다. 그런데 Extended Isolatoin Forest에서는 random slope의 개념을 도입하여 "non-axis-parallel split"을 도입합니다.
Motivation
Non-axis-parallel split을 도입한 이유는 기존 Isolation Forest로 계산한 anomaly score가 일관되지 않다 (inconsistent)는 것입니다. 즉, anomaly score가 robust하지 않다는 것이죠. 밑에 두가지 예를 통해 이를 확인할 수 있습니다.
실험은 다음과 같이 진행됩니다.
- 구조를 알고 있는 synthetic 데이터를 생성한다.
- 이 데이터를 이용해 Isolation Forest를 training 시킨다.
- train된 Isolation Forest를 이용해 모든 점 (특정 범위에 대해 유니폼 분포에서 생성한)들에 대한 anomaly score를 계산한다.
- 계산된 anomaly score값을 기반으로 contour plot을 그려 anomaly score map을 시각화한다.
1. Normally distributed data
2차원 평면에 평균이 (0,0) 인 정규분포로 부터 생성된 데이터가 있습니다.

이 데이터를 이용해 Isolation Forest를 training 시킨 후
모든 점들에 대해 계산된 anomaly score가 같은 점들을 이은 anomaly score map (contour plot)은 아래와 같습니다.
(밝을수록 anomaly score가 높고 어두울수록 값이 낮습니다.)

데이터가 정규분포로 부터 생성되었기 때문에, 우리는 Isolation Forest로 계산한 anomaly score의 contour plot 역시 원형을 그리며 값이 작아지길 기대합니다. 그런데 실제 관측된 anomaly score는 [-2,2] 범위에선 원형의 형태를 보이지만, 그 범위를 벗어나면 원형이 아닌 직사각형의 양상을 보이는 걸 확인할 수 있습니다.
이럴경우, $x_{1}, x_{2}$는 원점 (0,0)으로 부터 떨어진 반지름은 같지만 anomaly score는 서로 다른 결과가 발생하게 됩니다.
즉, 같은 반지름에 대해서 anomaly score의 분산이 커지는 문제가 발생하는 것이죠.
2. Two normally distributed clusters
이번엔 같은 2차원 평면에서 평균이 (0,10)인 정규분포와 (10,0)인 정규분포 두개로 부터 생성된 데이터의 경우를 보겠습니다.

이 경우, 2개의 확연한 클러스터가 발생하는 걸 확인할 수 있습니다.
이 데이터를 이용하여 Isolation Forest를 training 시킨 후,
모든 점들에 대해 계산된 anomaly score가 같은 점들을 이은 anomaly score map (contour plot)은 아래와 같습니다.
(밝을수록 anomaly score가 높고 어두울수록 값이 낮습니다.)
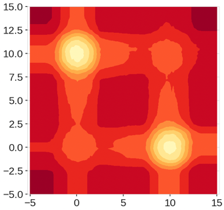
두 클러스터의 중심점 (0,10), (10,0) 주변엔 기대한 대로 원형의 contour plot이 형성되었지만
1번의 예와 마찬가지로 어떠한 범위를 넘어가자 직사각형 형태의 contour plot이 형성된 걸 확인할 수 있습니다.
또한 이보다 더 심각한 문제는 (0,0), (10,10)을 중심으로 마치 데이터들이 모여있는 것 처럼 보이는 "Ghost Cluster"가 생성되었다는 것입니다. 이 ghost cluster는 자칫 정상 point를 anomaly로 분류하게 하여 "false alarm rate"을 높이는 것 뿐 아니라 원래 데이터 구조에 대한 bias를 만들어 낸다는 점에서 심각한 문제가 됩니다.
위의 두 예를 통해, Isolation Forest가 생성하는 anomaly score가 robust 하지 않다 (anomaly score의 분산이 크다)는 것을 확인했습니다. 다음 장에선, 이 문제가 발생하는 원인이 무엇인지에 대해 알아보겠습니다.
What Makes This Problem?
위에서 본 문제의 원인은 Isolation Forest의 split 작동 방식에 있습니다.
Isolation Forest는 각 노드에서 랜덤하게 선택한 변수 하나와 그 변수가 가지는 범위에서의 criterion 값 하나를 이용하여 feature space를 partition 합니다.
이 때의 split은 그 정의상, 특정 축에 평행한 axis-pararell 하다는 제약조건이 있습니다.
그리고 이 제약조건이 바로 위에서 관측한 문제의 근원 원인이 됩니다.
아래의 그림은 위에서 살펴본 두가지 예에 대하여 각각 하나의 iTree를 적합시켰을 때의 모습을 나타냅니다.

그림을 보면, 2차원 평면이기 때문에 split의 방향은 가로, 세로 두가지 뿐입니다.
1번 그림을 보면, 관측값들이 모여있는 중심부에서 split이 많이 이루어지는 걸 볼 수 있습니다. 데이터가 많이 모여있을 수록 isolation 시키려면 많은 split이 필요할 수 밖에 없겠죠. 그런데 문제는 축 방향이 두가지 뿐이기 때문에 중심부의 데이터를 isolation 시키기 위해 많은 split이 적용되는 과정에서 데이터가 없는 지역에도 여러번의 split이 가해진다는 것입니다. (3,0), (3,1.8) 부근이 대표적인 예 입니다.
2번 그림 역시, 데이터가 모여있는 클러스터에서 많은 split이 발생하는데 이 때, split 과정에서 데이터가 존재하지 않는 지역에 많은 split이 적용되는 걸 볼 수 있습니다. (10,10)이 대표적인 예 입니다.
위의 예를 통해 축과 평행한 axis-parallel 제약 조건이 데이터가 존재하지 않는 구역에 대한 anomaly score를 높인다는 것을 확인했습니다. 다음으로 이 문제를 해결하기 위한 방법을 소개합니다.
Solution
Extended Isolation Forest는 위의 문제를 해결하기 위한 방안으로 "non-axis-parallel" split을 제안합니다.
non-axis-parallel split은 split이 이루어지는 방식에 어떠한 제약도 걸지 않고 feature space를 랜덤으로 partition 하는 방법입니다.
아래의 그림이 그 예시 입니다.

이를 이용해 위의 두가지 예에 대하여 iTree를 적합했을 때의 모습은 아래와 같습니다.
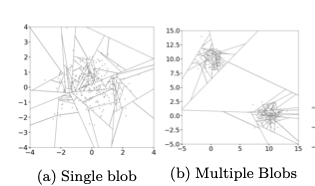
위 그림의 결과를 보면, 기존 axis-parallel split에서 발생했던 데이터 포인트들이 몰려있는 곳을 isolation 시키기 위해 다른 지역에 split이 많이 적용되던 문제가 해결된 것을 확인할 수 있습니다. 두 그림 모두 중심부 이외의 지역에 split이 특별히 많이 적용된 곳이 없다는 것을 볼 수 있습니다.
non-axis-parallel split을 적용하는 방법은 간단합니다.
-
Let $\mathfrak{X}\in\mathbb{R}^{d}$
-
Let $\vec{d}\in\mathbb{R}^{d}$ be a direction vector
-
Draw a random number for each coordinate of $\vec{d}$ from $\mathcal{N}(0,1)$ which is the standard normal distribution
-
For the intercept, $\vec{p}$, we simply draw from a uniform distribution over the range of values present at each branching point
-
The branching criteria for the data splitting for a given point $\vec{x}$ is as follows:
$(\vec{x}-\vec{p})\cdot\vec{d}\leq0$
-
위 조건을 만족하는 데이터 포인트 $\vec{x}$는 왼쪽 child node로 이동되고 그렇지 않은 데이터 포인트들은 오른쪽 노드로 옮겨진다.
Notation
-
$X=\{x_{1},\cdots,x_{n}\}, \quad x_{i}\in\mathbb{R}^{d}$ for all $i=1,\cdots,N$
-
$T$: a node of an isolation tree
-
$h(x)$: path length of $x$ (iTree에서 isolation 되는데 사용된 split 횟수)
-
$E(h(x))$: average path length of $x$ ($x$가 각 iTree에서 isolation 되는 데 사용된 path length들의 평균)
-
$c(n)$: $h(x)$를 normalize 하기 위해 사용된 상수. (average path length of unsuccessful search in BST (Binary Search Tree)[B. R. Presis, 1999]).
$c(n) = 2H(n-1) - (2(n-1)/n)$,
where $H(i) \approx ln(i) + 0.5772156649$
-
s(x,n): anomaly score
$s(x,n) = 2^-{E(h(x))\over c(n) }$
When $E(h(x)) \rightarrow c(n), \quad s \rightarrow 0.5$
When $E(h(x)) \rightarrow 0, \quad s \rightarrow 1$
When $E(h(x)) \rightarrow n-1, \quad s \rightarrow 0$
=> $s(x,n)$ 를 정의한 이유는 $E(h(x))$를 [0,1]로 bound 시키기 위함입니다.
$E(h(x))$가 클수록 anomaly score인 $s(x,n)$은 0에 가까워지고
$E(h(x))$가 작을수록 anomaly score인 $s(x,n)$은 1에 가까워지게 됩니다.
이 값을 기준으로 모든 데이터 포인트들의 anomaly score를 계산하여 서로 비교할 수 있게 됩니다.
Algorithm
Extended Isolation forest의 알고리즘은 split 방법을 제외하곤 기존 Isolation Forest와 동일합니다.
알고리즘은 2단계로 나눠서 진행됩니다.
1) Training stage
2) Evaluation stage
Training stage에선 input data $X$를 이용해 $t$개의 sub-sample과 iTree를 만들어서 iForest로 ensemble 해줍니다.
Evaluation stage에선 Training stage에서 생성한 $t$개의 iTree에 대해 모든 데이터 포인트 $x$의 path length를 계산합니다. 여기서 계산된 path length를 기반으로 각 데이터 포인트의 anomaly score를 도출합니다.
Training stage

1. iForest를 저장할 빈 객체 생성
2. tree의 heigh limit 설정
3. for loop (sub-sampling 갯수 $t$ 회 반복)
4. sub-sampling (sub-samping size: $\psi$)
5. iTree construction & iForest에 저장
6. end for loop
7. return iForest

1. sampling 된 $X^{'}$이 isolaiton 된다면 external node로 return
4. direction 벡터 $\vec{n}$을 뽑는다. (각 coordinate들을 표준정규분포로부터 뽑는다)
5. $X$의 범위 중 intercept 포인트 $\vec{p}$를 랜덤하게 선택한다.
6. Extension level에 따라 direction 벡터 $\vec{n}$의 coordinate 값을 0으로 조정한다.
7. $(X-\vec{p})\cdot\vec{n}\leq0)$을 만족하는 $x$들을 $X_{\ell}$로 배정
8. 위의 조건에 해당하지 않는 $x$들을 $X_{r}$로 할당
9. 모든 데이터 포인트가 isolation 될 때까지 iTree 반복. split 될 때마다 그 정보 $(\vec{n}, \vec{p})$ 저장.
Evaluation stage

만들어진 iTree에 데이터 포인트 하나인 $x$를 흘려보낸다.
1. 현재 $\vec{x}$가 있는 노드가 external node (terminal node) 일 경우, $e + c(T.size)$를 return
$e$: 현재 path length
$c(T.size)$ 현재 노드에 있는 데이터 포인트 갯수로 계속 split 했을 때 기대되는 path length. 이걸 더해주는 이유는
위의 Training stage에서 height limit에 걸려 tree split이 멈춘 경우 그 노드를 external node로 return 하는데, 그 노드 안에 1개가 아닌 여러 개의 데이터 포인트가 존재할 수 있다. split을 멈추지 않고 계속했을 때의 사전에 기대되는 path length를 $c(T.size)$로 계산해 더해준다.
4. 현재 노드 $T$에 저장되어 있는 direction 벡터를 $\vec{n}$으로 선언한다.
5. 현재 노드 $T$에 저장되어 있는 intercept 벡터를 $\vec{p}$로 선언한다.
6. 만약 데이터 포인트 $\vec{x}$가 $(\vec{x}-\vec{p})\cdot\vec{n}\leq0$을 만족하면 현재 노드 $T$의 왼쪽 노드인 $T.left$로 흘려보내고 다시 path length 알고리즘을 적용한다.
8. $(\vec{x}-\vec{p})\cdot\vec{n}\geq0$일 경우, 현재 노드 $T$의 오른쪽 노드인 $T.right$로 $x$를 흘려보내고 다시 path length 알고리즘을 작동시킨다.
=> 위의 Algorithm3를 통해 모든 데이터 포인트의 path length를 구할 수 있다. 이를 $t$ 개의 iTree에 적용한 후 average 하면 모든 데이터 포인트에 대해 average path length 인 $E(h(x))$를 얻을 수 있다. 이를 이용해 최종적으로 Anomaly score 인 $s(x,n)$을 얻는다.
Empirical Results
Synthetic Data
위의 알고리즘을 통해 계산한 Extended Isolation Forest의 anomaly score 값과 기존 (standard) Isolation Forest의 anomaly score 값을 비교한 아래의 그림을 통해 Extended Isolation Forest가 기존 Isolation Forest의 문제를 극복했다는 것을 확인할 수 있습니다.


Extended Isolation Forest의 경우 직사각형의 contour plot이 생기는 문제가 사라졌고 2개의 클러스터가 있는 경우에 발생하는 "Ghost Cluster" 역시 사라진 것을 확인할 수 있습니다.
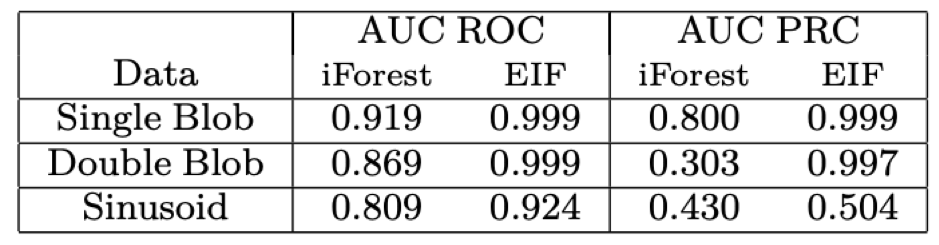
또한 Anomaly Detecting의 성과 지표 중 하나인 ROC 커브와 PRC 커브에서의 AUC 역시 Extended Isolation Forest가 우수하다는 것을 관측할 수 있습니다.
Real Data
예제로 사용한 synthetic 데이터 말고 실제 Anomaly Detection 문제가 있는 Real Data 에서 두 알고리즘 Isolation Forest와 Extended Isolation Forest의 결과를 비교해보죠.
우선 사용된 데이터는 다음과 같습니다.

이 6가지 데이터셋에 대해 각각 Isolation Forest와 Extended Isolation Forest를 적합시켜 얻은 결과는 아래와 같습니다.

근소하게 Extended Isolation Forest의 결과가 더 좋은 걸 확인할 수 있습니다.
(주의: 이 데이터셋에 한정하여 이런 결과가 나타난 것입니다. 모든 상황에서 Extended Isolation Forest가 Isolation Forest보다 우세하다고 결로낼 수 없습니다.)
Conclusion
Extended Isolation Forest는 Isolation Forest의 axis-parallel split이 가지는 약점을 보완하기 위해 제시된 테크닉 입니다.
본문에선 특정 상황에서 Isolation Forest의 anomaly score가 robust 하지 않다는 걸 확인했고 이러한 문제가 axis-parallel split 이라는 제약조건 때문에 발생한다는 것을 봤습니다.
이를 해결하기 위해 non-axis-parallel split을 소개하였고 이를 적용하였을 때, 극복하고자 했던 문제가 해결된 것을 확인했습니다.
Future wokrs:
생각해볼 수 있는 발전 방향은 다음과 같습니다.
-
dimensionality reduction (either feature selection or feature extraction) for anomaly detection in high dimensional data
-
Dealing with categorical variables
References
- Hariri, Sahand, Matias Carrasco Kind, and Robert J. Brunner. ”Extended isolation forest.” arXiv preprint arXiv:1811.02141 (2018).
- Liu, Fei Tony, Kai Ming Ting, and Zhi-Hua Zhou. ”Isolation forest.” In 2008 Eighth IEEE International Conference on Data Mining, pp. 413-422. IEEE, 2008.



